Square root of 2

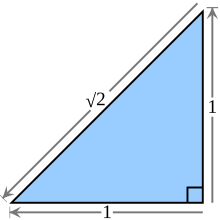
The square root of 2 is equal to the length of the hypotenuse of an isosceles right triangle with legs of length 1.
Representations
Decimal	1.4142135623730950488...
Continued fraction	${\displaystyle 1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}}$
Binary	1.01101010000010011110...
Hexadecimal	1.6A09E667F3BCC908B2F...

The square root of 2 (approximately 1.4142) is a positive real number that, when multiplied by itself, equals the number 2. It may be written in mathematics as ${\displaystyle {\sqrt {2}}}$ or ${\displaystyle 2^{1/2}}$. It is an algebraic number, and therefore not a transcendental number. Technically, it should be called the principal square root of 2, to distinguish it from the negative number with the same property.

Geometrically, the square root of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem. It was probably the first number known to be irrational. ^[1] The fraction 99/70 (≈ 1.4142857) is sometimes used as a good rational approximation with a reasonably small denominator.

Sequence A002193 in the On-Line Encyclopedia of Integer Sequences consists of the digits in the decimal expansion of the square root of 2, here truncated to 65 decimal places: ^[2]

1.41421356237309504880168872420969807856967187537694807317667973799

History

The Babylonian clay tablet YBC 7289 ( c. 1800–1600 BC) gives an approximation of ${\displaystyle {\sqrt {2}}}$ in four sexagesimal figures, 1 24 51 10, which is accurate to about six decimal digits, ^[3] and is the closest possible three-place sexagesimal representation of ${\displaystyle {\sqrt {2}}}$:

${\displaystyle 1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}={\frac {305470}{216000}}=1.41421{\overline {296}}.}$

Another early approximation is given in ancient Indian mathematical texts, the Sulbasutras ( c. 800–200 BC), as follows: Increase the length [of the side] by its third and this third by its own fourth less the thirty-fourth part of that fourth. ^[4] That is,

${\displaystyle 1+{\frac {1}{3}}+{\frac {1}{3\times 4}}-{\frac {1}{3\times 4\times 34}}={\frac {577}{408}}=1.41421{\overline {56862745098039}}.}$

This approximation is the seventh in a sequence of increasingly accurate approximations based on the sequence of Pell numbers, which can be derived from the continued fraction expansion of ${\displaystyle {\sqrt {2}}}$. Despite having a smaller denominator, it is only slightly less accurate than the Babylonian approximation.

Pythagoreans discovered that the diagonal of a square is incommensurable with its side, or in modern language, that the square root of two is irrational. Little is known with certainty about the time or circumstances of this discovery, but the name of Hippasus of Metapontum is often mentioned. For a while, the Pythagoreans treated as an official secret the discovery that the square root of two is irrational, and, according to legend, Hippasus was murdered for divulging it. ^{[5] [6]} The square root of two is occasionally called Pythagoras's number or Pythagoras's constant, for example by Conway & Guy (1996). ^[7]

Ancient Roman architecture

In ancient Roman architecture, Vitruvius describes the use of the square root of 2 progression or ad quadratum technique. It consists basically in a geometric, rather than arithmetic, method to double a square, in which the diagonal of the original square is equal to the side of the resulting square. Vitruvius attributes the idea to Plato. The system was employed to build pavements by creating a square tangent to the corners of the original square at 45 degrees of it. The proportion was also used to design atria by giving them a length equal to a diagonal taken from a square, whose sides are equivalent to the intended atrium's width. ^[8]

Decimal value

Computation algorithms

There are many algorithms for approximating ${\displaystyle {\sqrt {2}}}$ as a ratio of integers or as a decimal. The most common algorithm for this, which is used as a basis in many computers and calculators, is the Babylonian method ^[9] for computing square roots. It goes as follows:

First, pick a guess, ${\displaystyle a_{0}>0}$; the value of the guess affects only how many iterations are required to reach an approximation of a certain accuracy. Then, using that guess, iterate through the following recursive computation:

${\displaystyle a_{n+1}={\frac {a_{n}+{\frac {2}{a_{n}}}}{2}}={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}.}$

The more iterations through the algorithm (that is, the more computations performed and the greater "n"), the better the approximation. Each iteration roughly doubles the number of correct digits. Starting with ${\displaystyle a_{0}=1}$, the results of the algorithm are as follows:

• 1 (a₀)
• 3/2 = 1.5 (a₁)
• 17/12 = 1.416... (a₂)
• 577/408 = 1.414215... (a₃)
• 665857/470832 = 1.4142135623746... (a₄)

The product of pi and the square root of two can be calculated through the following BBT-style formula: ^[10]

${\displaystyle \pi {\sqrt {2}}={\frac {1}{8}}\sum _{k=0}^{\infty }{\frac {1}{64^{k}}}({\frac {32}{12k+1}}+{\frac {8}{2k+3}}+{\frac {8}{12k+5}}-{\frac {4}{12k+7}}-{\frac {1}{12k+9}}-{\frac {1}{12k+11}})}$

Rational approximations

A simple rational approximation 99/70 (≈ 1.4142857) is sometimes used. Despite having a denominator of only 70, it differs from the correct value by less than 1/10,000 (approx. +0.72×10⁻⁴).

The next two better rational approximations are 140/99 (≈ 1.4141414...) with a marginally smaller error (approx. −0.72×10⁻⁴), and 239/169 (≈ 1.4142012) with an error of approx −0.12×10⁻⁴.

The rational approximation of the square root of two derived from four iterations of the Babylonian method after starting with a₀ = 1 (665,857/470,832) is too large by about 1.6×10⁻¹²; its square is ≈ 2.0000000000045.

Records in computation

In 1997, the value of ${\displaystyle {\sqrt {2}}}$ was calculated to 137,438,953,444 decimal places by Yasumasa Kanada's team. In February 2006, the record for the calculation of ${\displaystyle {\sqrt {2}}}$ was eclipsed with the use of a home computer. Shigeru Kondo calculated one trillion decimal places in 2010. ^[11] Among mathematical constants with computationally challenging decimal expansions, only π, e, and the golden ratio have been calculated more precisely as of March 2022 ^[update]. ^[12] Such computations aim to check empirically whether such numbers are normal.

This is a table of recent records in calculating the digits of ${\displaystyle {\sqrt {2}}}$. ^[12]

Date	Name	Number of digits
January 5, 2022	Tizian Hanselmann	10000000001000
June 28, 2016	Ron Watkins	10000000000000
April 3, 2016	Ron Watkins	5000000000000
January 20, 2016	Ron Watkins	2000000000100
February 9, 2012	Alexander Yee	2000000000050
March 22, 2010	Shigeru Kondo	1000000000000

Proofs of irrationality

A short proof of the irrationality of ${\displaystyle {\sqrt {2}}}$ can be obtained from the rational root theorem, that is, if ${\displaystyle p(x)}$ is a monic polynomial with integer coefficients, then any rational root of ${\displaystyle p(x)}$ is necessarily an integer. Applying this to the polynomial ${\displaystyle p(x)=x^{2}-2}$, it follows that ${\displaystyle {\sqrt {2}}}$ is either an integer or irrational. Because ${\displaystyle {\sqrt {2}}}$ is not an integer (2 is not a perfect square), ${\displaystyle {\sqrt {2}}}$ must therefore be irrational. This proof can be generalized to show that any square root of any natural number that is not a perfect square is irrational.

For other proofs that the square root of any non-square natural number is irrational, see Quadratic irrational number or Infinite descent.

Proof by infinite descent

One proof of the number's irrationality is the following proof by infinite descent. It is also a proof of a negation by refutation: it proves the statement "${\displaystyle {\sqrt {2}}}$ is not rational" by assuming that it is rational and then deriving a falsehood.

1. Assume that ${\displaystyle {\sqrt {2}}}$ is a rational number, meaning that there exists a pair of integers whose ratio is exactly ${\displaystyle {\sqrt {2}}}$.
2. If the two integers have a common factor, it can be eliminated using the Euclidean algorithm.
3. Then ${\displaystyle {\sqrt {2}}}$ can be written as an irreducible fraction ${\displaystyle {\frac {a}{b}}}$ such that a and b are coprime integers (having no common factor) which additionally means that at least one of a or b must be odd.
4. It follows that ${\displaystyle {\frac {a^{2}}{b^{2}}}=2}$ and ${\displaystyle a^{2}=2b^{2}}$.   (  (a/b)ⁿ = aⁿ/bⁿ )   ( a² and b² are integers)
5. Therefore, a² is even because it is equal to 2b². (2b² is necessarily even because it is 2 times another whole number.)
6. It follows that a must be even (as squares of odd integers are never even).
7. Because a is even, there exists an integer k that fulfills ${\displaystyle a=2k}$.
8. Substituting 2k from step 7 for a in the second equation of step 4: ${\displaystyle 2b^{2}=a^{2}=(2k)^{2}=4k^{2}}$, which is equivalent to ${\displaystyle b^{2}=2k^{2}}$.
9. Because 2k² is divisible by two and therefore even, and because ${\displaystyle 2k^{2}=b^{2}}$, it follows that b² is also even which means that b is even.
10. By steps 5 and 8, a and b are both even, which contradicts step 3 (that ${\displaystyle {\frac {a}{b}}}$ is irreducible).

Since we have derived a falsehood, the assumption (1) that ${\displaystyle {\sqrt {2}}}$ is a rational number must be false. This means that ${\displaystyle {\sqrt {2}}}$ is not a rational number; that is to say, ${\displaystyle {\sqrt {2}}}$ is irrational.

This proof was hinted at by Aristotle, in his Analytica Priora, §I.23. ^[13] It appeared first as a full proof in Euclid's Elements, as proposition 117 of Book X. However, since the early 19th century, historians have agreed that this proof is an interpolation and not attributable to Euclid. ^[14]

Proof by unique factorization

As with the proof by infinite descent, we obtain ${\displaystyle a^{2}=2b^{2}}$. Being the same quantity, each side has the same prime factorization by the fundamental theorem of arithmetic, and in particular, would have to have the factor 2 occur the same number of times. However, the factor 2 appears an odd number of times on the right, but an even number of times on the left—a contradiction.

Geometric proof

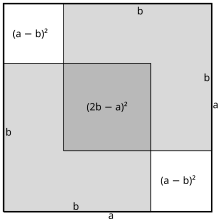
A simple proof is attributed to Stanley Tennenbaum when he was a student in the early 1950s. ^{[15] [16]} Given two squares with integer sides respectively a and b, one of which has twice the area of the other, place two copies of the smaller square in the larger as shown in Figure 1. The square overlap region in the middle (${\displaystyle (2b-a)^{2}}$) must equal the sum of the two uncovered squares (${\displaystyle 2(a-b)^{2}}$). However, these squares on the diagonal have positive integer sides that are smaller than the original squares. Repeating this process, there are arbitrarily small squares one twice the area of the other, yet both having positive integer sides, which is impossible since positive integers cannot be less than 1.

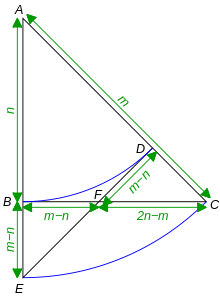
Tom M. Apostol made another geometric reductio ad absurdum argument showing that ${\displaystyle {\sqrt {2}}}$ is irrational. ^[17] It is also an example of proof by infinite descent. It makes use of classic compass and straightedge construction, proving the theorem by a method similar to that employed by ancient Greek geometers. It is essentially the same algebraic proof as in the previous paragraph, viewed geometrically in another way.

Let △ ABC be a right isosceles triangle with hypotenuse length m and legs n as shown in Figure 2. By the Pythagorean theorem, ${\displaystyle {\frac {m}{n}}={\sqrt {2}}}$. Suppose m and n are integers. Let m:n be a ratio given in its lowest terms.

Draw the arcs BD and CE with centre A. Join DE. It follows that AB = AD, AC = AE and ∠BAC and ∠DAE coincide. Therefore, the triangles ABC and ADE are congruent by SAS.

Because ∠EBF is a right angle and ∠BEF is half a right angle, △ BEF is also a right isosceles triangle. Hence BE = m − n implies BF = m − n. By symmetry, DF = m − n, and △ FDC is also a right isosceles triangle. It also follows that FC = n − (m − n) = 2n − m.

Hence, there is an even smaller right isosceles triangle, with hypotenuse length 2n − m and legs m − n. These values are integers even smaller than m and n and in the same ratio, contradicting the hypothesis that m:n is in lowest terms. Therefore, m and n cannot be both integers; hence, ${\displaystyle {\sqrt {2}}}$ is irrational.

Constructive proof

While the proofs by infinite descent are constructively valid when "irrational" is defined to mean "not rational", we can obtain a constructively stronger statement by using a positive definition of "irrational" as "quantifiably apart from every rational". Let a and b be positive integers such that 1<a/b< 3/2 (as 1<2< 9/4 satisfies these bounds). Now 2b² and a² cannot be equal, since the first has an odd number of factors 2 whereas the second has an even number of factors 2. Thus |2b² − a²| ≥ 1. Multiplying the absolute difference |√2 − a/b| by b²(√2 + a/b) in the numerator and denominator, we get ^[18]

${\displaystyle \left|{\sqrt {2}}-{\frac {a}{b}}\right|={\frac {|2b^{2}-a^{2}|}{b^{2}\!\left({\sqrt {2}}+{\frac {a}{b}}\right)}}\geq {\frac {1}{b^{2}\!\left({\sqrt {2}}+{\frac {a}{b}}\right)}}\geq {\frac {1}{3b^{2}}},}$

the latter inequality being true because it is assumed that 1<a/b< 3/2, giving a/b + √2 ≤ 3 (otherwise the quantitative apartness can be trivially established). This gives a lower bound of 1/3b² for the difference |√2 − a/b|, yielding a direct proof of irrationality in its constructively stronger form, not relying on the law of excluded middle; see Errett Bishop (1985, p. 18). This proof constructively exhibits an explicit discrepancy between ${\displaystyle {\sqrt {2}}}$ and any rational.

Proof by Pythagorean triples

This proof uses the following property of primitive Pythagorean triples:

If a, b, and c are coprime positive integers such that a² + b² = c², then c is never even. ^[19]

This lemma can be used to show that two identical perfect squares can never be added to produce another perfect square.

Suppose the contrary that ${\displaystyle {\sqrt {2}}}$ is rational. Therefore,

${\displaystyle {\sqrt {2}}={a \over b}}$

where ${\displaystyle a,b\in \mathbb {Z} }$ and ${\displaystyle \gcd(a,b)=1}$

Squaring both sides,

${\displaystyle 2={a^{2} \over b^{2}}}$

${\displaystyle 2b^{2}=a^{2}}$

${\displaystyle b^{2}+b^{2}=a^{2}}$

Here, (b, b, a) is a primitive Pythagorean triple, and from the lemma a is never even. However, this contradicts the equation 2b² = a² which implies that a must be even.

Multiplicative inverse

The multiplicative inverse (reciprocal) of the square root of two (i.e., the square root of 1/2) is a widely used constant.

${\displaystyle {\frac {1}{\sqrt {2}}}={\frac {\sqrt {2}}{2}}=\sin 45^{\circ }=\cos 45^{\circ }=}$ 0.70710678118654752440084436210484903928483593768847...   (sequence A010503 in the OEIS)

One-half of ${\displaystyle {\sqrt {2}}}$, also the reciprocal of ${\displaystyle {\sqrt {2}}}$, is a common quantity in geometry and trigonometry because the unit vector that makes a 45° angle with the axes in a plane has the coordinates

${\displaystyle \left({\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right)\!.}$

This number satisfies

${\displaystyle {\tfrac {1}{2}}{\sqrt {2}}={\sqrt {\tfrac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos 45^{\circ }=\sin 45^{\circ }.}$

Properties

One interesting property of ${\displaystyle {\sqrt {2}}}$ is

${\displaystyle \!\ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1}$

since

${\displaystyle \left({\sqrt {2}}+1\right)\!\left({\sqrt {2}}-1\right)=2-1=1.}$

This is related to the property of silver ratios.

${\displaystyle {\sqrt {2}}}$ can also be expressed in terms of copies of the imaginary unit i using only the square root and arithmetic operations, if the square root symbol is interpreted suitably for the complex numbers i and −i:

${\displaystyle {\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}{\text{ and }}{\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}}$

${\displaystyle {\sqrt {2}}}$ is also the only real number other than 1 whose infinite tetrate (i.e., infinite exponential tower) is equal to its square. In other words: if for c > 1, x₁ = c and x_n+1 = c^x_n for n > 1, the limit of x_n as n → ∞ will be called (if this limit exists) f(c). Then ${\displaystyle {\sqrt {2}}}$ is the only number c > 1 for which f(c) = c². Or symbolically:

${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{~\cdot ^{~\cdot ^{~\cdot }}}}}=2.}$

${\displaystyle {\sqrt {2}}}$ appears in Viète's formula for π:

${\displaystyle 2^{m}{\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}\to \pi {\text{ as }}m\to \infty }$

for m square roots and only one minus sign. ^[20]

Similar in appearance but with a finite number of terms, ${\displaystyle {\sqrt {2}}}$ appears in various trigonometric constants: ^[21]

${\displaystyle {\begin{aligned}\sin {\frac {\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}&\quad \sin {\frac {3\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}&\quad \sin {\frac {11\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}}\\[6pt]\sin {\frac {\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}&\quad \sin {\frac {7\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}}&\quad \sin {\frac {3\pi }{8}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2}}}}\\[6pt]\sin {\frac {3\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}}&\quad \sin {\frac {\pi }{4}}&={\tfrac {1}{2}}{\sqrt {2}}&\quad \sin {\frac {13\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}}\\[6pt]\sin {\frac {\pi }{8}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2}}}}&\quad \sin {\frac {9\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}}&\quad \sin {\frac {7\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}\\[6pt]\sin {\frac {5\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}}&\quad \sin {\frac {5\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}&\quad \sin {\frac {15\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}\end{aligned}}}$

It is not known whether ${\displaystyle {\sqrt {2}}}$ is a normal number, which is a stronger property than irrationality, but statistical analyses of its binary expansion are consistent with the hypothesis that it is normal to base two. ^[22]

Representations

Series and product

The identity cos π/4 = sin π/4 = 1/√2, along with the infinite product representations for the sine and cosine, leads to products such as

${\displaystyle {\frac {1}{\sqrt {2}}}=\prod _{k=0}^{\infty }\left(1-{\frac {1}{(4k+2)^{2}}}\right)=\left(1-{\frac {1}{4}}\right)\!\left(1-{\frac {1}{36}}\right)\!\left(1-{\frac {1}{100}}\right)\cdots }$

and

${\displaystyle {\sqrt {2}}=\prod _{k=0}^{\infty }{\frac {(4k+2)^{2}}{(4k+1)(4k+3)}}=\left({\frac {2\cdot 2}{1\cdot 3}}\right)\!\left({\frac {6\cdot 6}{5\cdot 7}}\right)\!\left({\frac {10\cdot 10}{9\cdot 11}}\right)\!\left({\frac {14\cdot 14}{13\cdot 15}}\right)\cdots }$

or equivalently,

${\displaystyle {\sqrt {2}}=\prod _{k=0}^{\infty }\left(1+{\frac {1}{4k+1}}\right)\left(1-{\frac {1}{4k+3}}\right)=\left(1+{\frac {1}{1}}\right)\!\left(1-{\frac {1}{3}}\right)\!\left(1+{\frac {1}{5}}\right)\!\left(1-{\frac {1}{7}}\right)\cdots .}$

The number can also be expressed by taking the Taylor series of a trigonometric function. For example, the series for cos π/4 gives

${\displaystyle {\frac {1}{\sqrt {2}}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}\left({\frac {\pi }{4}}\right)^{2k}}{(2k)!}}.}$

The Taylor series of √1 + x with x = 1 and using the double factorial n!! gives

${\displaystyle {\sqrt {2}}=\sum _{k=0}^{\infty }(-1)^{k+1}{\frac {(2k-3)!!}{(2k)!!}}=1+{\frac {1}{2}}-{\frac {1}{2\cdot 4}}+{\frac {1\cdot 3}{2\cdot 4\cdot 6}}-{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6\cdot 8}}+\cdots =1+{\frac {1}{2}}-{\frac {1}{8}}+{\frac {1}{16}}-{\frac {5}{128}}+{\frac {7}{256}}+\cdots .}$

The convergence of this series can be accelerated with an Euler transform, producing

${\displaystyle {\sqrt {2}}=\sum _{k=0}^{\infty }{\frac {(2k+1)!}{2^{3k+1}(k!)^{2}}}={\frac {1}{2}}+{\frac {3}{8}}+{\frac {15}{64}}+{\frac {35}{256}}+{\frac {315}{4096}}+{\frac {693}{16384}}+\cdots .}$

It is not known whether ${\displaystyle {\sqrt {2}}}$ can be represented with a BBP-type formula. BBP-type formulas are known for π√2 and √2  ln(1+√2), however. ^[23]

The number can be represented by an infinite series of Egyptian fractions, with denominators defined by 2ⁿ th terms of a Fibonacci-like recurrence relation a(n) = 34a(n−1) − a(n−2), a(0) = 0, a(1) = 6. ^[24]

${\displaystyle {\sqrt {2}}={\frac {3}{2}}-{\frac {1}{2}}\sum _{n=0}^{\infty }{\frac {1}{a(2^{n})}}={\frac {3}{2}}-{\frac {1}{2}}\left({\frac {1}{6}}+{\frac {1}{204}}+{\frac {1}{235416}}+\dots \right)}$

Continued fraction

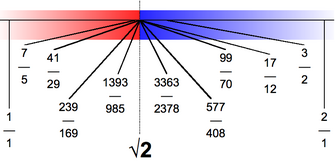
The square root of two has the following continued fraction representation:

${\displaystyle {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}.}$

The convergents p/q formed by truncating this representation form a sequence of fractions that approximate the square root of two to increasing accuracy, and that are described by the Pell numbers (i.e., p² − 2q² = ±1). The first convergents are: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408 and the convergent following p/q is p + 2q/p + q. The convergent p/q differs from ${\displaystyle {\sqrt {2}}}$ by almost exactly 1/2√2q², which follows from:

${\displaystyle \left|{\sqrt {2}}-{\frac {p}{q}}\right|={\frac {|2q^{2}-p^{2}|}{q^{2}\!\left({\sqrt {2}}+{\frac {p}{q}}\right)}}={\frac {1}{q^{2}\!\left({\sqrt {2}}+{\frac {p}{q}}\right)}}\thickapprox {\frac {1}{2{\sqrt {2}}q^{2}}}}$

Nested square

The following nested square expressions converge to ${\textstyle {\sqrt {2}}}$:

${\displaystyle {\begin{aligned}{\sqrt {2}}&={\tfrac {3}{2}}-2\left({\tfrac {1}{4}}-\left({\tfrac {1}{4}}-{\bigl (}{\tfrac {1}{4}}-\cdots {\bigr )}^{2}\right)^{2}\right)^{2}\\[10mu]&={\tfrac {3}{2}}-4\left({\tfrac {1}{8}}+\left({\tfrac {1}{8}}+{\bigl (}{\tfrac {1}{8}}+\cdots {\bigr )}^{2}\right)^{2}\right)^{2}.\end{aligned}}}$

Applications

Paper size

In 1786, German physics professor Georg Christoph Lichtenberg ^[25] found that any sheet of paper whose long edge is ${\displaystyle {\sqrt {2}}}$ times longer than its short edge could be folded in half and aligned with its shorter side to produce a sheet with exactly the same proportions as the original. This ratio of lengths of the longer over the shorter side guarantees that cutting a sheet in half along a line results in the smaller sheets having the same (approximate) ratio as the original sheet. When Germany standardised paper sizes at the beginning of the 20th century, they used Lichtenberg's ratio to create the "A" series of paper sizes. ^[25] Today, the (approximate) aspect ratio of paper sizes under ISO 216 (A4, A0, etc.) is 1:${\displaystyle {\sqrt {2}}}$.

Proof:
Let ${\displaystyle S=}$ shorter length and ${\displaystyle L=}$ longer length of the sides of a sheet of paper, with

${\displaystyle R={\frac {L}{S}}={\sqrt {2}}}$ as required by ISO 216.

Let ${\displaystyle R'={\frac {L'}{S'}}}$ be the analogous ratio of the halved sheet, then

${\displaystyle R'={\frac {S}{L/2}}={\frac {2S}{L}}={\frac {2}{(L/S)}}={\frac {2}{\sqrt {2}}}={\sqrt {2}}=R}$.

Physical sciences

There are some interesting properties involving the square root of 2 in the physical sciences:

• The square root of two is the frequency ratio of a tritone interval in twelve-tone equal temperament music.
• The square root of two forms the relationship of f-stops in photographic lenses, which in turn means that the ratio of areas between two successive apertures is 2.
• The celestial latitude (declination) of the Sun during a planet's astronomical cross-quarter day points equals the tilt of the planet's axis divided by ${\displaystyle {\sqrt {2}}}$.

See also

• List of mathematical constants
• Square root of 3, √3
• Square root of 5, √5
• Gelfond–Schneider constant, 2^√2
• Silver ratio, 1 + √2

Notes

References

• Apostol, Tom M. (2000), "Irrationality of the square root of two – A geometric proof", American Mathematical Monthly, 107 (9): 841–842, doi: 10.2307/2695741, JSTOR  2695741.
• Aristotle (2007), Analytica priora, eBooks@Adelaide
• Bishop, Errett (1985), Schizophrenia in contemporary mathematics. Errett Bishop: reflections on him and his research (San Diego, Calif., 1983), 1–32, Contemp. Math. 39, Amer. Math. Soc., Providence, RI.
• Flannery, David (2005), The Square Root of Two, Springer-Verlag, ISBN  0-387-20220-X.
• Fowler, David; Robson, Eleanor (1998), "Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context", Historia Mathematica, 25 (4): 366–378, doi: 10.1006/hmat.1998.2209.
• Good, I. J.; Gover, T. N. (1967), "The generalized serial test and the binary expansion of ${\displaystyle {\sqrt {2}}}$", Journal of the Royal Statistical Society, Series A, 130 (1): 102–107, doi: 10.2307/2344040, JSTOR  2344040.
• Henderson, David W. (2000), "Square roots in the Śulba Sūtras", in Gorini, Catherine A. (ed.), Geometry At Work: Papers in Applied Geometry, Cambridge University Press, pp. 39–45, ISBN  978-0-88385-164-7.

External links

• Gourdon, X.; Sebah, P. (2001), "Pythagoras' Constant: ${\displaystyle {\sqrt {2}}}$", Numbers, Constants and Computation.
• The Square Root of Two to 5 million digits by Jerry Bonnell and Robert J. Nemiroff. May, 1994.
• Square root of 2 is irrational, a collection of proofs
• Grime, James; Bowley, Roger. "The Square Root ${\displaystyle {\sqrt {2}}}$ of Two". Numberphile. Brady Haran.
• √2 Search Engine 2 billion searchable digits of √2, π and e